Magnetic field energy

A magnetic field is characterised by the energy parameter. If we turn the switch S to position 2 (Figure 33), the current in the circuit will not disappear, because there are still some additional currents in the circuit due to the self-inductance phenomena. This means that some part of the charge will be moved along the circuit.

This will partially be characterised by the energy stored in the circuit. The fragment of work is

$dA={\epsilon }_{S}dq=LI\frac{dl}{dt}$

Thus

$A=\int dA=L\int I\frac{dl}{dt}=L{I}^2/2$

So the energy stored in the magnetic field is

$W_m=\frac{L{I}^2}{2}$

Magnetic field energy is represented through the magnetic field. B is

$W_m=\frac{L{I}^2}{2}=\frac{1}{2}\mu {\mu }_0{n}^{2}V(\frac{B}{\mu {\mu }_{0}n}{)}^2=\frac{B^2}{2\mu {\mu }_0}V$

V is a solenoid volume.

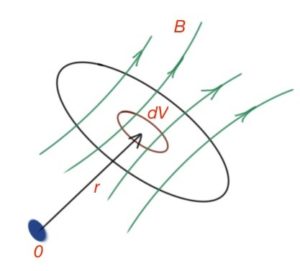
Energy of the fragment of space within the magnetic field is

$w_m=\frac{d{W}_m}{dV}$

(Figure 34). The magnetic field inside of the solenoid is uniform, so

$w_m=\frac{W_m}{V}=\frac{B^2}{2\mu {\mu }_0}$

W_m  is the volume energy density of the magnetic field. In case of a non-uniform field you can use this formula to determine the volume energy of the fragment of the field. In the case of a magnetic field as a function, if the coordinates is known then we can determine the volume energy for any fragment of the space Ω:

$W_m=\frac{1}{2\mu {\mu }_0}{\int }_{\Omega }{B}^2\left(r\right)dV$

Magnetic field in the matter